Variables, caractères statistiques: types de variables, représentations graphiques et tabulaires.
Représentations graphiques
La deuxième étape du processus descriptif est celui du tracé d'une représentation graphique de la distribution de la variable. Nous ne décrirons ici que quelques techniques de représentation graphique.
Diagrammes circulaires.
Les diagrammes circulaires se présentent sous la forme d'un disque dont les secteurs ont une mesure dont le pourcentage par rapport à celle du secteur total (360°) est égal à la fréquence de chacune des valeurs de la variable.
Le calcul des mesures des angles s'effectue comme suit : fréquence x 360°
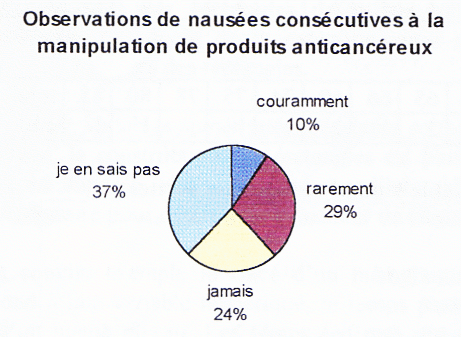
Ce graphique est utile en ce qu'il permet une vision parfois plus simple des informations recueillies par le tableau : prédominance de la réponse je ne sais pas équivalence des réponses jamais et rarement Faible importance de la réponse couramment En revanche il est parfois délicat d'estimer les relations numériques entre effectifs â l'aide ce graphique (le secteur correspondant à rarement est trois fois plus grand que celui qui correspond à couramment )
Diagrammes
Les diagrammes en bâton sont les représentations graphiques les plus simples â tracer et à décrire.
Ces diagrammes en bâton sont constitués de bâtons comme leur nom l'indique. Chaque trait est associé à une des valeurs de la variable. Ces bâtons sont de longueur proportionnelle à l'effectif (ou à la fréquence de la valeur représentée.
Si la variable n'est pas numérique les bâtons sont disposés à intervalles réguliers sur une droite horizontale et cette disposition n'est adoptée que parce qu'elle favorise l'appréhension visuelle.
Si la variable est numérique, on porte sur l'axe horizontal les valeurs de la variable. Les bâtons s'élèvent au dessus des valeurs dont ils représentent les effectifs.
La description d'un tel diagramme (dans le cas où la variable est numérique) s'appuie sur les relevés visuels suivants :
Identification des éventuelles concentrations d'effectifs C'est-à-dire des zones du dessin où les traits sont contiguës et élevés. Réciproquement, on détermine les creux d'effectifs, c'est-à-dire les zones du dessin où les traits sont clairsemées et peu élevés.
La tache que représente l'ensemble des bâtons peut être symétrique ou encore asymétrique.
La courbe qu'esquissent les extrémités des bâtons peut être croissante ou décroissante.
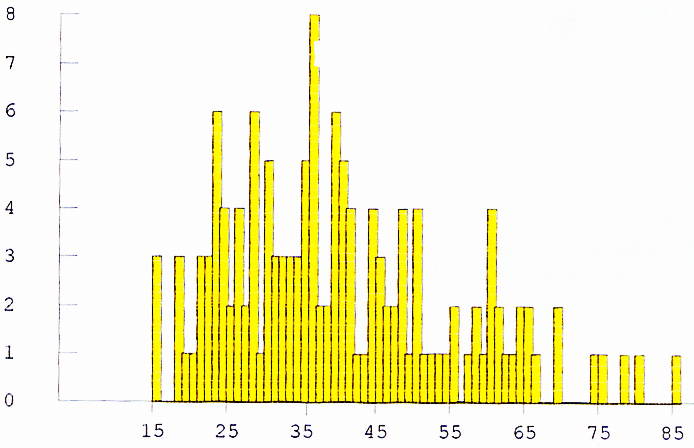
Une description de la série numérique s'appuyant sur le diagramme construit peut être : On observe une relative concentration des textes les plus courts opposée à une toute aussi relative dispersion des textes les plus longs. On observe également une nette asymétrie de la distribution vers les valeurs les plus basses. Enfin la courbe formée par les extrémités, des bâtons du diagramme est tout d'abord croissante jusqu'à la valeur 36 d'effectif 8 puis décroissante. La croissance est relativement forte la décroissance au contraire plutôt douce.
Toutes ces observations vont dans le même sens à savoir une opposition entre la relative homogénéité des textes courts composés par un grand nombre d'élèves et l'hétérogénéité des textes longs , composés par un nombre moindre d'élèves. Histogrammes.
On désigne par ce nom les représentations graphiques où l'effectif de chacune des valeurs de la variable est visualisé par un rectangle.
La seule règle de construction de ces rectangles est que l'aire d'un rectangle doit être proportionnelle à l'effectif (ou à la fréquence). Si comme c'est souvent le cas les rectangles sont construits sur du papier millimétré/quadrillé à petits carreaux, cette règle exige de commencer par déterminer le nombre d'individus que représente 1 cm²/ un petit carreau.
Premier cas : variables autres que numériques.
Dans ce cas, ta construction des rectangles représentant les effectifs de chacune des valeurs prises est simple. On choisit l'échelle c'est-à-dire le nombre d'individus que représente un petit carreau puis des rectangles de même base. La hauteur du rectangle est alors proportionnelle à l'effectif de la catégorie ainsi qu'à la fréquence. L'oeil n'a plus qu'à s'attacher aux hauteurs des rectangles.
Deuxième cas : variables numériques présentées sous forme d'intervalles.
Dans ce cas, la construction des rectangles est plus complexe. En effet la base de chaque rectangle est imposée (elle se confond avec l'intervalle numérique). Par conséquent un calcul va être nécessaire pour déterminer la hauteur de chacun des rectangles.
Il faut calculer les hauteurs des rectangles, en effectuant le quotient des aires par les bases correspondantes.
